Exploring the World of Magnets

In this article, we will delve into the basics of magnets, including their properties, types of materials, and some fun activities to explore their behavior.
Magnetic and Non-Magnetic Materials
One of the most interesting aspects of magnets is their ability to attract certain materials.
Materials that are attracted to magnets are called magnetic materials, such as iron, nickel, and cobalt.
These materials contain specific atomic structures that align with a magnet’s field, creating an attraction.
On the other hand, materials like wood, plastic, rubber, and glass are non-magnetic because their atomic structures do not respond to magnetic fields.
This distinction is essential in understanding where magnets can be effectively used and where they cannot.
Poles of a Magnet
Every magnet has two ends, known as poles: the north pole and the south pole.
The poles are where the magnetic force is the strongest. If you break a magnet into smaller pieces, each piece will still have a north and a south pole, no matter how small it gets.
One fascinating property of poles is that like poles repel each other (north repels north, and south repels south), while opposite poles attract (north attracts south).
This behavior forms the basis of many practical applications, such as in electric motors and magnetic locks.
Fun fact: A magnetic pole cannot exist without the existence of the opposite pole. So if there is a North pole there MUST be a South pole. And, if there is a South pole there MUST be a North pole. A single magnetic pole also called a “monopole” is only a mathematical entity and has not yet been discovered to exist in the observable physical universe.
Finding Directions
Before the invention of GPS, magnets played a crucial role in navigation. The Earth itself acts like a giant magnet with its magnetic north and south poles.
A simple compass made with a small, magnetized needle aligns itself with the Earth’s magnetic field, pointing toward the magnetic north.
.
This property has made magnets indispensable for travelers, sailors, and explorers throughout history.
Even today, compasses are vital tools for navigation in remote areas where electronic devices may fail.
Make Your Own Magnet (Hands-On Project)
Creating your own magnet is a fun and simple activity! Here’s how you can do it:
Take an iron nail or paperclip (a magnetic material).
Rub one end of the needle repeatedly in one direction with a strong magnet. Ensure you’re consistent with the direction of rubbing.
After a few minutes, the needle will become magnetized and can attract small objects like paper clips or pins.
This process, known as magnetization by stroking, aligns the tiny magnetic domains in the needle, turning it into a magnet.
You could also create a magnet by passing electricity through a metallic object by wrapping coils around the metal as shown above. This is called an electromagnet.
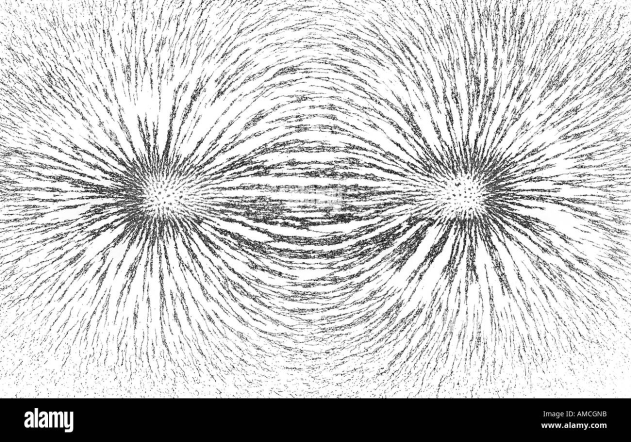
Attraction and Repulsion Between Magnets
Magnets exhibit a unique property of attraction and repulsion. When two magnets are brought close to each other:
●If their opposite poles face each other, they will attract.
This phenomenon can be easily observed by experimenting with two bar magnets.
The invisible magnetic field around the magnets causes this behavior, and it is the basis for many technological applications, such as maglev trains and magnetic levitation devices.
You can see the magnetic field by placing a magnet under a sheet of paper with iron filings as shown in the above image.
Applications of Magnets in the Modern World
Magnets play a critical role in modern technology and industry. Some key applications include:
●Electronics: Magnets are essential in devices like speakers, headphones, and microphones, where they help convert electrical energy into sound.
Conclusion
Magnets are not only intriguing but also incredibly useful in our daily lives.
Their ability to attract and repel, find directions, and perform various tasks makes them an essential part of both ancient and modern science.